[dropcap color=”#ef7f2c”]S[/dropcap] elama pemetaan gua, data yang diambil adalah panjang antar station dengan menggunakan pita ukur, sudut kemiringan antar station dengan menggunakan Clinometer, arah antar station dengan menggunakan Kompas, lebar lorong gua dengan menggunakan pita ukur, dan tinggi atap dengan menggunakan pita ukur.
Pada saat mengambil data tinggi atap gua, sering kali atap gua tidak bisa dijangkau karena terlalu tinggi. Untuk mengetahui berapa tinggi atap gua tersebut ada suatu cara dengan mengambil sudut kemiringan atap gua dari satu titik tertentu. Sama seperti cara mengukur ketinggian suatu gedung. Ada tiga informasi yang harus diketahui sebelum menghitung tinggi atap tersebut, yaitu jarak antara station (dimana tinggi atap yang akan dihitung) dengan station (tempat shooter), informasi yang kedua yang harus diketahui adalah sudut kemiringan dari station (tempat shooter) ke atap gua yang akan dihitung tingginya, informasi yang ketiga adalah tinggi station. Setelah mengetahui tiga informasi tersebut, maka kita bisa menggunakan rumus Pythagoras dan fungsi Trigonometri untuk menghitung tinggi atap gua tersebut.
Secara umum ada tiga kondisi di lapangan yang berbeda untuk menentukan bagaimana rumus Pythagoras dan Trigonometri digunakan. Kondisi pertama adalah jika antar station sejajar memiliki ketinggian yang sama atau rata-rata air, kondisi kedua adalah station pertama lebih tinggi posisinya dari pada station kedua, dan kondisi ketiga adalah jika station pertama lebih rendah posisinya dibanding station kedua.
Berikut adalah contoh kasus bagaimana menghitung tinggi atap suatu lorong gua.
1. Antar station sejajar
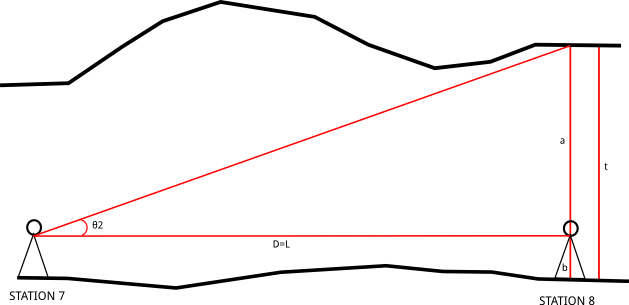
Antara STATION 7 dengan STATION 8 memiliki posisi yang sejajar.Yang diukur di lapangan adalah Jarak dari STATION 7 ke STATION 8 (D) 15 meter, kemudian sudut kemiringan dari STATION 7 ke atap gua di atas STATION 8 (θ2) sebesar 20º dan tinggi STATION (b) adalah 1 meter. Berapakah tinggi atap gua (t)?
Langkah pertama adalah mencari a.
a = D x TAN θ2
= 15 x TAN 20º
= 15 x 0.3639702342
= 5.46
Langkah kedua adalah mencari t.
t = a + b
= 5.46 + 1
= 6.46
Jadi, t atau tinggi atap gua pada STATION 8 adalah 6.46 meter.
2. Posisi STATION 1 lebih tinggi
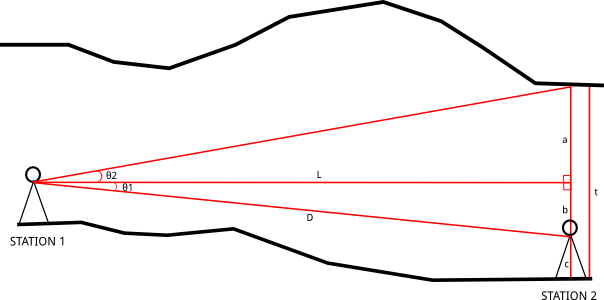
STATION 1 lebih tinggi dari pada STATION 2. Yang diukur di lapangan adalah Jarak dari STATION 1 ke STATION 2 (D) 15.3 meter, sudut kemiringan dari STATION 1 ke STATION 2 (θ1) sebesar 6º, sudut kemiringan dari STATION 1 ke atap di atas STATION 2 (θ2) sebesar 10º dan tinggi STATION (c) adalah 1 meter. Berapakah tinggi atap gua di atas STATION 2 (t)?
Langkah pertama adalah mencari b.
b = D x SIN θ1
= 15.3 x SIN 6º
= 15.3 x 0.10452846326
= 1.59
Langkah kedua mencari L.
L = D x COS θ1
= 15.3 x COS 6º
= 15.3 x 0.99452189536
= 15.21
Langkah ketiga adalah mencari a.
a = L x TAN θ2
= 15.21 x TAN 10º
= 15.21 x 0.17632698070
= 2.68
Langkah keempat adalah mencari t
t = a + b + c
= 2.68 + 1.59 + 1
= 5.27 meter
Jadi, tinggi atap gua diatas STATION 2 (t) adalah 5.27 meter.
3. Posisi STATION 3 lebih rendah
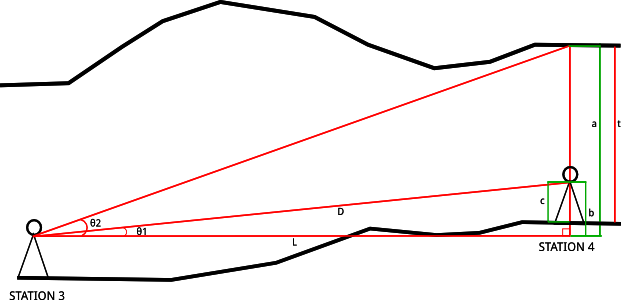
STATION 3 lebih rendah dari pada STATION 4. Yang diukur di lapangan adalah Jarak dari STATION 3 ke STATION 4 (D) 15 meter, sudut kemiringan dari STATION 3 ke STATION 4 (θ1) sebesar 5º, sudut kemiringan dari STATION 3 ke atap di atas STATION 4 (θ2) sebesar 20º dan tinggi STATION (c) adalah 1 meter. Berapakah tinggi atap gua di atas STATION 4 (t)?
Langkah pertama adalah mencari L.
L = D x COS θ1
= 15 x COS 5º
= 15 x 0.99619469469809
= 14.94 meter
Langkah kedua mencari b.
b = L x TAN θ1
= 14.94 x TAN 5º
= 14.94 x 0.0874886635
= 1.3 meter
Langkah ketiga mencari a.
a = L x TAN θ2
= 14.94 x TAN 20º
= 14.94 x 0.3639702342
= 5.4 meter
Langkah keempat mencari t.
t = (a – b) + c
= (5.4 – 1.3) + 1
= 4.1 + 1
= 5.1 meter
Jadi panjang t atau tinggi atap pada STATION 4 adalah 5.1 meter



mantab mas, menjadi lebih paham, ijin untuk share ya mas..
Silakan Mas Rasyid, semoga bermanfaat.
keren,, siph bgt… jadi lebih tau. kirain ngitung atap gua semua sama ternyata ada jenisnya. thanks
keren,, siph.. jadi lebih tau, kirain ngukur atap gua semua sama ternyata ada jenisnya,,. thanks
Sama-sama mbak Yulia